如图⊙O的两条_邬芳蕴同学数学作业《如图⊙O的两条》解题方法_数学_邬芳蕴

编辑： admin           2017-25-06         

如图⊙O的两条导读：

这道数学作业题来自邬芳蕴同学的作业解题方法分享《如图⊙O的两条》，指导老师是何老师，涉及到的数学知识点概括为：如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...，同学们可以通过学习如图⊙O的两条：如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...的相关数学知识来提升自己的数学作业解题能力，只有掌握了这些数学知识能力，才能让自己的数学解题能力提升，也才会在数学考试中取得良好的成绩，下面是邬芳蕴数学作业的详细总结概括分享（本道题以问答模式展开）。

题目：如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...

如图⊙O的两条：逆火学习站的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

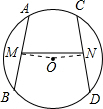证明：连OM，ON，如图，
∵M，N分别为AB，CD的中点，
∴OM⊥AB，ON⊥CD，
∴∠AMO=∠CNO=90°，
∵AB=CD，
∴OM=ON，
∴∠OMN=∠ONM，
∴∠AMN=∠CNM．

互助这道作业题的同学还参与了下面的作业题

题1： 【初三数学正方形ABCD中,AB=1.点P是射线DA上的一动点,DE⊥CP,垂足为E,EF⊥BE与射线DC交于点F.(1)若点P在边DA上(与点D,点A不重合)求证△DEF∽△CEB设AP=XDP=Y求Y与X的函数关系式,并写出函数定义域(2)当】[数学科目]

（1）①
∵∠DEC=∠FEB=90° ∴∠DEF=∠BEC （同角的余角相等） ∵∠EDF+∠DCP=90° ∠BCE+∠DCP=90° ∴∠EDF=∠BCE ∴△DEF∽△CEB ②∵在Rt△PDC中,DE⊥CP ∴∠CDP=∠CED=90° ∴△DEC∽△PDC ∴ DE/EC=PD/DC ∵△DEF∽△CEB ∴ DE/EC=DF/BC 又因BC=DC ∴ PD/DC=DF/DC ∴PD=DF ∵AP=x,DF=y ∴PD=1-x ∴y=1-x （0＜x＜1） （2）∵△DEF∽△CEB ∴ S△DEF/S△CEB=DF^2/CB^2.（1） ∵ S△DEF/S△CEF=DF/CF.（2） ∴用（1）/（2）式 得 S△CEF/S△CEB=DF•CF/CB2 又∵S△BEC=4S△EFC,∴ S△CEF/S△CEB=DF•CF/^CB2=1/4 当P点在边DA上时 有 (1-x)•x/1=1/4,解得 x=1/2 即:AP=1/2 当P点在边DA的延长线上时,(1+x)•x/1=1/4,解得 x=(√2-1)/2

如图⊙O的两条：逆火学习站的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

即:AP=(√2-1)/2

题2： 将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合.已知AB=2√3,P是AC上的一个动点.（1）当点P运动到∠ABC得平分线上时,连接DP,求DP的长.[数学科目]

（1）当点P运动到∠ABC得平分线上时,连接DP,求DP的长.
求DP 解法一：由题意,在 Rt△ABC 中, ∠ABC = 60° ,AB = 2√3, 由 sin∠ABC = AC / AB 得： AC = AB × sin∠ABC = 2√3 × sin60° = 2√3 × （√3/2） = 3由 cos∠ABC = BC / AB 得： BC = AB × cos∠ABC = AB × cos60° = 2√3 × （1/2） = √3∵ BP 平分 ∠ABC,∴ ∠PBC = （1/2）× ∠ABC = （1/2）× 60° = 30°在 Rt△PBC 中, PC = BC × tan∠PBC = BC × tan30° = √3 × (√3/3) = 1在等腰直角三角形ADC中,过点D 作DE ⊥ AC 与 点E,则：DE = EC = (1/2) × AC = (1/2) × 3 = 3/2∴ EP = EC -- PC = 3/2 -- 1 = 1/2在Rt△DEP 中,由勾股定理得： DP方 = DE方 + EP方 = (3/2)方 + (1/2)方 = 10 / 4∴ DP = √(10/4) = (√10) / 2以上解答中,您也可以由“在直角三角形中,30°所对的直角边等于斜边的一半”直接得出BC = AB/2 = √3.进而用勾股定理求出AC=3.求DP 解法二：适用高中知识“余弦定理”.在等腰直角△ADC中,DC = AC × cos∠DCA = AC × cos45° = 3 × (√2/2) = (3√2) / 2∴ DC方 = [ (3√2) / 2 ]方 = 9/2 ∴ DP方 = DC方 + PC方 -- 2 × DC × PC × cos∠DCA = 9/2 + 1 -- 2 × [ (3√2) / 2 ] × 1 × cos45° = 9/2 + 1 -- 2 × [ (3√2) / 2 ] × 1 × (√2/2) = 9/2 + 1 -- 3 = 5/2∴ DP = √(5/2) = (√10) / 2.（2）当点P在运动过程中出现DP=BC时, 此时∠PDA的度数为：15° 或 75° ,需分别讨论：在等腰直角三角形ADC中,∠DAP = 45°过点D 作DE ⊥ AC 与 点E,则：DE = EC = (1/2) × AC = (1/2) × 3 = 3/2 而DP = BC = √3 ∵ √3 ≠ 3/2 ,即 DP 与 DE 不重合、点P与点E不重合,∴ 当点P在运动过程中出现DP=BC时, 有两个时刻： ① 点P尚未越过 点E 前；② 点P越过 点E 之后. ① 点P尚未越过 点E 前： 在 Rt△DPE 中, sin∠DPE = DE / DP = (3/2) / √3 = √3 / 2 而 sin60° = √3 / 2 ∴ ∠DPE = 60°∴由 “三角形的一个外角等于与它不相邻的两个内角的和” 知： ∠DPE = ∠DAP + ∠PDA ∴∠PDA = ∠DPE -- ∠DAP = 60° -- 45° = 15° ② 点P越过 点E 之后： 在 Rt△DPE 中, sin∠DPE = DE / DP = (3/2) / √3 = √3 / 2 而 sin60° = √3 / 2 ∴ ∠DPE = 60° ,即：∠DPA = 60°在 △DPA 中,由三角形内角和定理得：∠PDA = 180° -- ∠DPE -- ∠DAP = 180° -- 60° -- 45° = 75°（3）顶点 “Q” 恰好在边BC上.您题中少打了 Q .当点P运动到AC的中点处时,以D、P、B、Q为顶点的平行四边形的顶点Q恰好在边BC上.理由如下：∵ 四边形DPBQ 是平行四边形∴ DP ‖ BQ 而 BQ ⊥ AC∴ DP ⊥ AC .即：DP是等腰Rt△DAC的底边AC 上的高.∴ 点P 此时为线段AC的中点.（等腰三角形底边上的高平分底边）∴当点P运动到AC的中点处时,以D、P、B、Q为顶点的平行四边形的顶点Q恰好在边BC上.求此时平行四边形DPBQ的面积：以 DP 为底,以 DP 与 BQ 间的 垂线段长 为高.DP 与 BQ （也可以说DP 与 BC）间的垂线段长即为PC.∵ DP ⊥ AC ∴ 点P为AC的中点∴ PC = DP = AC/2 = 3/2∴ S平行四边形DPBQ = DP × PC = (3/2) × (3/2)

如图⊙O的两条：逆火学习站的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

= 9/4

题3： 某校数学课外活动探究小组，在老师的引导下进一步研究了完全平方公式.结合实数的性质发现以下规律：对于任意正数a、b，都有a+b≥2ab成立.某同学在做一个面积为3600cm2，对角线相互垂直[数学科目]

由题意得：

1

2

ab
=3600，
则ab=7200，
所以有a+b≥2

7200

，
即a+b≥120

2

．
故选A．

题4： 如图，甲、乙两只捕捞船同时从A港出海捕鱼．甲船以每小时152千米的速度沿西偏北30°方向前进，乙船以每小时15千米的速度沿东北方向前进．甲船航行2小时到达C处，此时甲船发现渔具丢在[数学科目]

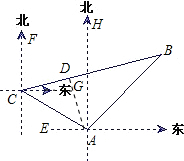（1）如图，过A作AD⊥BC于点D．作CG∥AE交AD于点G．
∵乙船沿东北方向前进，
∴∠HAB=45°，
∵∠EAC=30°，
∴∠CAH=90°-30°=60°
∴∠CAB=60°+45°=105°．
∵CG∥EA，∴∠GCA=∠EAC=30°．
∵∠FCD=75°，∴∠BCG=15°，∠BCA=15°+30°=45°，
∴∠B=180°-∠BCA-∠CAB=30°．
在直角△ACD中，∠ACD=45°，AC=2×15

2

=30

2

．
AD=AC?sin45°=30

2

×

2

2

=30千米．
CD=AC?cos45°=30千米．
在直角△ABD中，∠B=30°．
则AB=2AD=60千米．
则甲船从C处追赶上乙船的时间是：60÷15-2=2小时；
（2）BC=CD+BD=30+30

3

千米．
则甲船追赶乙船的速度是每小时（30+30

3

）÷2=15+15

3

千米/小时．
答：甲船从C处追赶上乙船用了2小时，甲船追赶乙船的速度是每小时15+15

3

千米．

题5： 如图,在菱形ABCD中,∠B=60°,∠EAF绕点A旋转,且∠EAF=60°(1)如图1,若∠EAF与菱形ABCD的两边BC和CD分别相交于点E、F.请你证明：∠BAE=∠CEF(2)如图2,若∠EAF与菱形ABCD的两边BC和CD的延长线分别相交于点E[数学科目]

初三现在没学四点共圆,现改用三角形全等方法.
题目中图1没给,可自己画一个∠EAF在∠BAD内,显然∠BAE和∠CEF是锐角,不可互补只能相等.题目（1）没问题.

如图⊙O的两条：逆火学习站的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

(1)连结AC,由菱形性质易知∠B=∠ACF=60°,AB=AC,∠BAC=∠EAF=60°,再同时减去∠EAC就得到∠BAE=∠CAF.从而△ABE≌△ACF,得AE=AF又∠EAF=60°有△AEF是等边三角形.再由三角形外角性质知∠AEF=∠B+∠BAE=60°+∠BAE,∠AEG=∠AEF+∠CEF=60°+∠CEF从而由等式性质得：∠BAE=∠CEF. 
(2)∠BAE与∠CEF互补

如图⊙O的两条：逆火学习站的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

由类似（1）方法知△ACE≌△ADF,得AE=AF又∠EAF=60°有△AEF是等边三角形.从而∠ACD=∠AEF=60°再由三角形外角性质知∠CAE+∠CEA=60°.因此∠BAC+∠CAE+∠CEA +∠AEF=180°即∠BAE与∠CEF互补.

如图⊙O的两条：逆火学习站(img1.72589.com)的邬芳蕴同学的作业题：《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》解题思路

如图⊙O的两条小结：

通过以上关于邬芳蕴同学对如图⊙O的两条：如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...的概括总结详细分享，相信同学们已经对如图⊙O的两条的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结，仔细揣摩邬芳蕴同学分享的解答《如图，⊙O中两条不平行弦AB和CD的中点M，N.且AB=CD，求...》这道作业题的重点部分，他山之石，可以攻玉，考才获胜。

•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克