已知园c和y相切_林有幕同学数学作业《已知园c和y相切》解题方法_数学_林有幕
编辑: admin 2017-25-06
-
4
已知园c和y相切导读:
这道数学作业题来自林有幕同学的作业解题方法分享《已知园c和y相切》,指导老师是谭老师,涉及到的数学知识点概括为:已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...,同学们可以通过学习已知园c和y相切:已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...的相关数学知识来提升自己的数学作业解题能力,只有掌握了这些数学知识能力,才能让自己的数学解题能力提升,也才会在数学考试中取得良好的成绩,下面是林有幕数学作业的详细总结概括分享(本道题以问答模式展开)。
题目:已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...
设直线l的方程为x/a+y/b=1,即bx+ay-ab=0,圆C的标准方程为(x-1)^2+(y-1)^2=1,圆心C(1,1),半径r=1.(1)直线l与圆C相切,则根号|b+a-ab|/ (a2+b2)=1,∴(a-2)(b-2)=2(4分)(2)设线段AB的中点M(x,y),则x=a/2,y=b/2 ,即a=2x,b=2y,代入(a-2)(b-2)=2,得(x-1)(y-1)=1/2 (x>1,y>1)(3)S△AOB=1/2|ab|=a+b-1=(a-2)+(b-2)+3≥2根号(a-2)(b-2) +3=2根号2+3已知园c和y相切:逆火学习站的林有幕同学的作业题:《已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...》解题思路
当且仅当a=b=2+根号2时,△AOB的面积最小,最小值为2根号2+3互助这道作业题的同学还参与了下面的作业题
题1: 已知与曲线C:x2+y2-2x-2y+1=0相切的直线L分别交x轴,y轴于A(a,0),B(0,b)两点(a>2,b>2),求线段AB中点的轨迹方程[数学科目]
(x-1)^2+(y-1)^2=1圆心(1,1),半径=1直线x/a+y/b=1bx+ay-ab=0圆心到切线距离=半径所以|b+a-ab|/√(a^2+b^2)=1(a+b-ab)^2=a^2b^2AB中点x=a/2,y=b/2a=2x,b=2y代入(2x+2y-4xy)^2=4x^2+4y^2x^2+y^2+4x^2y^2+2xy-4x^2y-4xy^2=x^2+y^22x^2y^2+xy-2x^2y-2xy^2=0a,b都不等于0所以x,y也不等于02xy+1-2x-2y=0已知园c和y相切:逆火学习站的林有幕同学的作业题:《已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...》解题思路
其中x=a/2>1,y=b/2>1题2: 已知与曲线C:x2+y2-2x-2y+1=0相切的直线l交x轴、y轴于A、B两点,O为原点,且|OA|=a,|OB|=b,(a>2,b>2).(1)求证:曲线C与直线l相切的条件是(a-2)(b-2)=2;(2)求线段AB中点的轨迹方程[数学科目]
(1)证明:由题意知,直线l的方程为| x |
| a |
| y |
| b |
即bx+ay-ab=0.
曲线C的方程配方得(x-1)2+(y-1)2=1,
∴直线l与圆C相切的充要条件是1=
| |a+b?ab| | ||
|
整理得ab-2a-2b+2=0,
即(a-2)(b-2)=2;
(2)设AB的中点为M(x,y),
则由中点坐标公式得:a=2x,b=2y,代入(a-2)(b-2)=2,得
(2x-2)(2y-2)=2,
即 (x-1)(y-1)=
| 1 |
| 2 |
∴线段AB中点的轨迹方程为:(x-1)(y-1)=
| 1 |
| 2 |
题3: 已知曲线C:X2+Y2-2X-2Y+1=0相切的直线L交X,Y轴的正半轴AB两点,O为原点,若|OA|=a,|OB|=b(a>2,b>2)(1)求[数学科目]
S=1/2ab则ab=2S而(a-2)(b-2)=2即ab-2(a+b)+2=0整理得到ab+2=2(a+b)>=2x2√ab即2S+2>=4√2S令t=√2S则t^2=2S(t>=0)于是上式可化为t^2-4t+2=0则t=2+√2已知园c和y相切:逆火学习站的林有幕同学的作业题:《已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...》解题思路
即√2S=2+√2故S=3+√2(当且仅当a=b=2+√2取等号)题4: 已知圆A:x2+y2+2x+2y-2=0,若圆B平分圆A的周长,且圆B的圆心在直线l:y=2x上,求满足上述条件的半径最小的圆B的方程.[数学科目]
设圆B的半径为r,∵圆B的圆心在直线l:y=2x上,∴圆B的圆心可设为B(t,2t);圆A的方程变成:(x+1)2+(y+1)2=4,圆心A(-1,-1),设圆A,圆B交于C,D两点,∵圆B平分圆A的周长,∴圆心A在CD上,如下图所示:
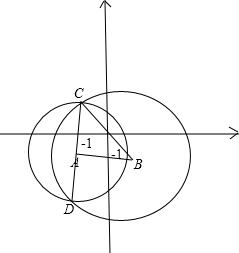 连接BA,BC,则△ABC是直角三角形,|BC|=r,|AC|=2;
连接BA,BC,则△ABC是直角三角形,|BC|=r,|AC|=2;∴(t+1)2+(2t+1)2+4=r2,整理得:r2=5t2+6t+6=5(t+
| 3 |
| 5 |
| 21 |
| 5 |
∴t=?
| 3 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
|
∴圆B的方程为(x+
| 3 |
| 5 |
| 6 |
| 5 |
| 21 |
| 5 |
题5: 把直线x-2y+λ=0向左平移1个单位,再向下平移2个单位后,与曲线x2+y2+2x-4y=0正好相切,则实数λ的值为
解析:直线x-2y+λ=0变形,y=x/2+λ/2向左平移1个单位,再向下平移2个单位后,得y=(1/2)(x+1)+λ/2-2=x/2+λ/2-3/2在变形:直线x-2y+λ-3=0曲线x2+y2+2x-4y=0变形(x+1)^2+(y-2)^2=5说明以(-1,2)为圆心,半径为根号5因为相切,可以用圆心点到直线公式=半径,所以已知园c和y相切:逆火学习站(img1.72589.com)的林有幕同学的作业题:《已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...》解题思路
已知园c和y相切小结:
通过以上关于林有幕同学对已知园c和y相切:已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...的概括总结详细分享,相信同学们已经对已知园c和y相切的相关数学作业知识一定有所收获吧。建议同学们要学会归纳总结,仔细揣摩林有幕同学分享的解答《已知与曲线C:x2+y2-2x-2y+1=0相切的直线L.分别交x轴,...》这道作业题的重点部分,他山之石,可以攻玉,考才获胜。
