【质量均为m的小球a】如图所示,质量均为m的小球A、B用两根不可伸长的轻绳..._物理_谢晋宇1029
编辑: admin 2017-15-06
-
4
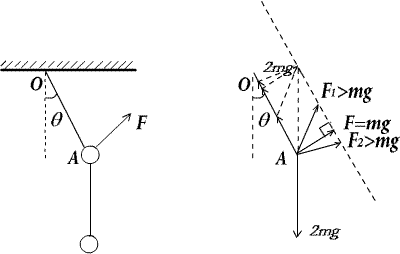
如图,为使两小球处于静止 状态且悬线OA与竖直方向的夹角保持30度不变,则外力F的方向可以沿F1、F2和F等多个方向,但各个方向的大小各不相同,以沿F方向为最小,大小等于mg.而A答案3分之根号3 mg,小于mg,所以不可能.
互助这道作业题的同学还参与了下面的作业题
题1: 如图所示,质量均为m的小球A、B用两根不可伸长的轻绳连接后悬挂于O点,在外力F的作用下,小球A、B处于静止,若要使两小球处于静止状态且悬线OA与竖直方向的夹角保持30度不变,则外力F的大小[物理科目]
由于只知外力的大概方向(易知F与悬线几乎共线时其大小几乎无穷大,最小是F竖直向上时)
所以有F≥mg
所以有BCD
题2: 如图所示,质量为m的小球用细线悬挂在小车上,小车的质量为M,当水平外力拉小车沿光滑水平面水平向右做匀加速运动时,悬线与竖直方向成30°角,此时:(1)小车的加速度是多大?(2)悬线中[物理科目]
(1):建立直角坐标系:绳子对小球的拉力为f1;小球的重力为:mg,根据受力分析可知:绳子的拉力沿竖直方向的分量 f1cos30=mg,(1)沿着水平方向的分量为:f1sin30=ma,(2 )其中a
为小球的加速度.解方程(1),(2)得:a=gtan30 ..由于小车与小球的运动状态相同,故小车的加速度也为:gtan30.
(2),由(1)可知,f1=mg/cos30.
题3: 质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到Q点,则力F所做的功为为什么列式为-mgL(1-cosθ)+W=0绳的拉力不做功吗动能定理中的W指什么不[物理科目]
小球在水平拉力F(是变力)作用下,是沿圆弧缓慢移动的(类似圆周运动,只是速度极小),所以拉力不做功.
由动能定理 得 W总=0-0
即各力做功之和等于物体动能的变化量.
W重+W水平拉=0
可见,-mgL(1-cosθ) +W=0 中的W是指水平力F做的功.
题4: 【一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平拉力F作用下,从平衡位置P点很缓慢地移动到O点力F】[物理科目]
首先,“从平衡位置 P 点很缓慢地移动到O点”意思是说忽略小球的速度,即可以认为小球的速度始终是零,小球始终处于平衡的状态,在这个过程中只发生一种能量转换,即F对小球做功,转化为小球的重力势能.
这样一来,要求F做功,有两种思路:1)直接用做功公式来求;2)用能量转换的思路来做,即求小球重力势能增加了多少,这部分能量就是由F做功而来.
这里先说第二种方法,结果为mgl(1-cosa),你已经懂了.
再说第一种方法,你的思路是不错的,Flsin(角) ,但是你忽略了一个问题,在小球移动的过程中F不是一个恒力!简单做个力合成图可以看出在这个过程中F是越变越大的,所以你用公式 Flsin(角)就不合适了.等到将来你学了微积分,用这种思路你就可以做了, 把力F与水平方位移关系找到,然后用这个变力在水平位移上进行积分就行了.
另外,多说一点,即使用第二种方法把问题解决了,通过比较这两种方法可以看出,第一种方法要比第二种方法简单的多,既然有更简便的方法,我们何必再去用复杂的方法呢,是吧?
题5: 【一质量为m的小球,用长为L的轻绳悬挂在O点,小球在水平恒力F作用下,从静止开始由平衡位置P点移动到Q点,此时绳与竖直方向的偏角为θ如图所示,则力F所做的功为()A.mgLcosθB.mgL】[物理科目]
由功的公式可知,W=FLcosθ=F?LPQcosθ
由几何关系可知,LPQcosθ=Lsinθ
故拉力的功为:W=FLsinθ
故选:C
