【秦九韶算法】【秦九韶算法怎么算?举几个例子】_数学_87541113Q群km
编辑: admin 2017-15-06
-
4
秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法.在西方被称作霍纳算法.
秦九韶算法是一种将一元n次多项式的求值问题转化为n个一次式的算法.其大大简化了计算过程,即使在现代,利用计算机解决多项式的求值问题时,秦九韶算法依然是最优的算法.
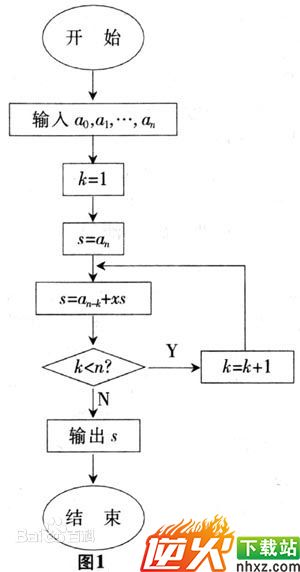
一般地,一元n次多项式的求值需要经过[n(n+1)]/2次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法.在人工计算时,一次大大简化了运算过程.
把一个n次多项式f(x)=a[n]x^n+a[n-1]x^(n-1)+.+a[1]x+a[0]改写成如下形式
f(x)=a[n]x^n+a[n-1]x^(n-1))+.+a[1]x+a[0]
=(a[n]x^(n-1)+a[n-1]x^(n-2)+.+a[1])x+a[0]
=((a[n]x^(n-2)+a[n-1]x^(n-3)+.+a[2])x+a[1])x+a[0]
=.
=(.((a[n]x+a[n-1])x+a[n-2])x+.+a[1])x+a[0].
求多项式的值时,首先计算最内层括号内一次多项式的值,即 v[1]=a[n]x+a[n-1] 然后由内向外逐层计算一次多项式的值,即
v[2]=v[1]x+a[n-2]
v[3]=v[2]x+a[n-3]
.
v[n]=v[n-1]x+a[0]
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.(注:中括号里的数表示下标)
结论:对于一个n次多项式,至多做n次乘法和n次加法.

互助这道作业题的同学还参与了下面的作业题
题1: 秦九韶算法运算次数如果用秦九韶算法计算n次多项式的值,则需要几次乘法,几次加法?请写得详细一些[数学科目]
这有学习软件,关于秦九韶算法
题2: 什么是秦九韶算法[数学科目]
秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法.在西方被称作霍纳算法(Horner algorithm或Horner scheme),是以英国数学家威廉·乔治·霍纳命名的.
把一个n次多项式f(x)=a[n]x^n+a[n-1]x^(n-1)+.+a[1]x+a[0]改写成如下形式:
f(x)=a[n]x^n+a[n-1]x^(n-1))+.+a[1]x+a[0]
=(a[n]x^(n-1)+a[n-1]x^(n-2)+.+a[1])x+a[0]
=((a[n]x^(n-2)+a[n-1]x^(n-3)+.+a[2])x+a[1])x+a[0]
=.
=(.((a[n]x+a[n-1])x+a[n-2])x+.+a[1])x+a[0].
求多项式的值时,首先计算最内层括号内一次多项式的值,即
v[1]=a[n]x+a[n-1]
然后由内向外逐层计算一次多项式的值,即
v[2]=v[1]x+a[n-2]
v[3]=v[2]x+a[n-3]
.
v[n]=v[n-1]x+a[0]
这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.
(注:中括号里的数表示下标)
结论:对于一个n次多项式,至多做n次乘法和n次加法.
[编辑本段]意义
该算法看似简单,其最大的意义在于将求n次多项式的值转化为求n个一次多项式的值.在人工计算时,利用秦九韶算法和其中的系数表可以大幅简化运算;对于计算机程序算法而言,加法比乘法的计算效率要高很多,因此该算法仍有极大的意义,用于减少CPU运算时间.
题3: 【秦九韶算法怎么算】[数学科目]
例如求5*x的5次方+3*x的4次方+7*x的3次方+2x²+x+3
原式=(((((5x+3)x+4)x+7)x+2)x+1)x+3
这样就叫做秦九韶算法
题4: 用秦九韶算法计算f(x)=x^7-2x^6+3x^3-4x^2+1当x=2时,v4=_______?[数学科目]
那种算法是依次提取X
=x^2(x^5-2x^4+3x-4)+1
=x^2(x(x^4-2x^3+3)-4)+1
=x^2(x(x^3(x-2)+3)-4)+1
x=2
f(2)=7
