【直线y2x是三角形】直线y=2x是△ABC中∠C的平分线所在的直线，若A、B坐标..._数学_小司Ix68

编辑： admin 2017-15-06

由题意，点A关于直线y=2x的对称点A′在BC所在直线上，设A′点坐标为（x₁，y₁），则x₁、y₁满足

=-12

，即x₁=-2y₁．①

+22

=2?

?42

，即2x₁-y₁-10=0．②
解①②两式组成的方程组，得x₁=4，y₁=-2．
∴BC所在直线方程为y?1?2?1

=x?34?3

，
即3x+y-10=0．得
解方程组
3x+y-10=0，x=2，
y=2x，y=4．
∴所求C点坐标为（2，4）．
由题意|AB|²=50，|AC|²=40，|BC|²=10，
∴△ABC为直角三角形．

其他同学给出的参考思路：

C(a,2a)

因为是角分线，所以2-Kac/1+2*Kac=Kbc-2/1+2*Kab

Kac=2a-2/a+4

Kbc=2a-1/a-3

C(2,4)

Kac=1/3

Kbc=-3

Kac*Kbc=-1

所以是直角三角形

互助这道作业题的同学还参与了下面的作业题

题1：【直线Y=2X是三角形ABC中角C的平分线所在的直线方程,若A,B座标分别是A（-4,2）B（3,1）,求点C的座标并】[数学科目]

易知,点A(-4,2)关于直线y=2x的对称点是A’(4,-2).

由题设及对称性可知,点A’必在直线BC上,

可求得直线BC的方程:3x+y=10.

∴点C必是两条直线y=2x.3x+y=10的交点.

解这个方程组可得x=2,y=4.

∴点C（2,4）

题2：直线y=2x是三角形ABC的一个内角平分线所在地直线,若A.B两点坐标分别是A(-4,2),B(3,1),求点C的坐标.

设点C（a,2a）

AC=√(-4-a)²+(2-2a)²

BC=√(3-a)²+(1-2a)²

过点A和B向直线y=2x作垂线

垂足为E,F

AE=｜-8-2｜/√5=2√5

BF=｜6-1｜/√5=√5

因为y=2x是角平分线

那么

AE/AC=BF/BC

2√5/√(-4-a)²+(2-2a)²=√5/√(3-a)²+(1-2a)²

4/(16+8a+a²+4+4a²-8a)=1/(9-6a+a²+1-4a+4a²)

化简

3a²-8a+4=0

(3a-2)(a-2)=0

a=2/3或a=2

点C（2/3,4/3）或（2,4）

AB=√50

AC=√40

BC=√10

AB²=AC²+BC²

三角形ABC是直角三角形

C=90度

这是C（2,4）的情况,

当C为（2/3,4/3）的时候

cosC=-1（余弦定理）

其实

此时的点C是AB和角C的平分线的交点

简单写一下

直线AB：y-1=（1-2）/（3+4）×（x-3）即

x+7y-10=0

x=2y

联立交点（2/3,4/3）

所以此时的点C舍去

那么求的点C的坐标（2,4）

题3：直线y=2x是三角形ABC中角C的平分线所在的直线,若A,B的坐标分别为A(-4,2),B(3,1),求点C的坐标,并判断三[数学科目]

C(a,2a)

因为是角分线,所以2-Kac/1+2*Kac=Kbc-2/1+2*Kab

Kac=2a-2/a+4

Kbc=2a-1/a-3

C(2,4)

Kac=1/3

Kbc=-3

Kac*Kbc=-1

所以是直角三角形

题4：【已知直线y=2x是△ABC中∠C的平分线所在的直线，若A，B的坐标分别是A（-4，2），B（3，1），求点C的坐标．】[数学科目]

设点B关于直线y=2x的对称点为B′（x′，y′），则直线BB′⊥直线y=2x，且线段BB′的中点（3+x′2

，1+y′2

）在方程为y=2x的直线上，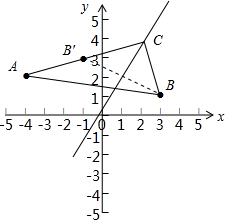

∴y′?1x′?3×2＝?1y′+12＝2×x′+32

，解得B′（-1，3）；
所以l_AB′：y-2=13

（x+4）；而点C为l_AB′：y-2=13

（x+4）与直线y=2x的交点，
∴y?2＝13(x+4)y＝2x

解得x＝2y＝4

，即点C的坐标为C（2，4）．

题5：直线y=2x是△ABC中∠C的平分线所在的直线，若A、B坐标分别为A（-4，2）、B（3，1），求点C的坐标，并判断△ABC的形状．[数学科目]