【如图a是圆o外一点】如图，a是圆o外一点，0a交圆o于点c，过圆o上一点p作pf垂..._数学_fuQL37KE93

编辑： admin           2017-15-06         

PA是圆o的切线

因为：角FpC=角cpA,在三角形PFC中,角FpC+角pCF=90

所以：角ApC+角pCF=90

又在三角形OPC中,角OPC=角PCO（角PCF）

所以：角ApC+角CPO=90

互助这道作业题的同学还参与了下面的作业题

题1： 【如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，弦DF与半径OB相交于点P，DE=23，∠DPA=45°，求OP的长．】[数学科目]

连接OD，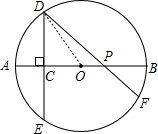
设⊙O的半径为R，
∵弦DE垂直平分半径OA，
∴OC=AC=12

R，
∵DE⊥AB，AB为直径，
∴DC=CE=12
DE=12
×23
=3
，
在Rt△DCO中，由勾股定理得：OD²=DC²+OC²，
R²=（12
R）²+（3
）²，
解得：R=2，
∴OC=12
R=1，
∵DE⊥AB，
∴∠DCF=90°，
∵∠DPA=45°，
∴∠CDP=45°=∠DPA，
∴CP=DC=3
，
∴OP=CP-OC=3
-1．

题2： 如图,AB是圆O的直径,以OA为直径的圆O1与圆O的弦AC相交于D,de⊥oc,垂足为E1、求证AD=dc2、求证de是○O1的切线3如果oe=ec,请说明四边形O1OED是什么四边形[数学科目]

1,连结od,bc;∠oda=∠bca=90度.od平行于bc,o是ab中点,所以d是ac中点,AD=dc.

2,找到oa的中点f,f是圆O1的圆心,连结fd,fd平行于oc,因为de⊥oc,所以de⊥fd,de是○O1的切线.

3,正方形.

题3： 如图,AB为圆的直径,OC垂直AB,垂足为O,点E、F、G在圆O上,分别作GM垂直OA,GN垂直OC,EH垂直OC,EK垂直OB,FQ垂直OC,FP垂直OB,垂足分别为M、N、H、K、Q、P,试比较MN、QP、HK的大小[数学科目]

矩形的对角线相等：

连接OB、OE、OF,

那MN=OB,HK=OE,PQ=OF,

∵OB=OE=OF,

∴MN=HK=PQ.

题4： 【如图,直线AB,CD相交于与点O,∠AOC=30°,半径为1cm的圆P的圆心在直线OA上,且与点O的距离为6cm,如果圆P的圆心在直线OA上,且与点O的距离为6cm,如果圆P以1cm/s的速度沿由A向B的方向移动,那么多少秒后】[数学科目]

不对,相切时圆心到线距离为一,则圆心到O距离（斜边）为二,则移动了四或八厘米,则时间一样出来了.

题5： 如图，⊙O的半径为3厘米，点B为⊙O外一点，OB交⊙O于点A，且AB=OA，动点P从点A出发，以π厘米/秒的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为（）秒时，直线[数学科目]


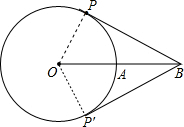
连接OP，
∵直线BP与⊙O相切，
∴OPB=90°，
∵AB=OA=OP，
∴OB=2OP，
∴∠PBO=30°，
∴POB=60°，
∴弧AP的长是60π?3180

=π，
即时间是π÷π=1（秒）；
当在P′点时，直线BP与⊙O相切，
此时弧APP′的长是(360?60)π?3180
=5π，
即时间是5π÷π=5（秒）；
故选D．
•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克