【已知bc平行oa】已知，BC∥OA，∠B=∠A=100°，试回答下列问题：(1)如图..._数学_傻叉250105
编辑： admin 2017-15-06
-
4
（1）证明：∵BC∥OA，
∴∠B+∠O=180°，
∴∠O=180°-∠B=80°，
而∠A=100°，
∴∠A+∠O=180°，
∴OB∥AC；
（2）∵OE平分∠BOF，
∴∠BOE=∠FOE，
而∠FOC=∠AOC，
∴∠EOF+∠COF=12
（3）不改变．
∵BC∥OA，
∴∠OCB=∠AOC，∠OFB=∠AOF，
∵∠FOC=∠AOC，
∴∠AOF=2∠AOC，
∴∠OFB=2∠OCB，
即∠OCB：∠OFB的值为1：2；
（4）设∠AOC的度数为x，则∠OFB=2x，
∵∠OEB=∠AOE，
∴∠OEB=∠EOC+∠AOC=40°+x，
而∠OCA=180°-∠AOC-∠A=180°-x-100°=80°-x，
∵∠OEB=∠OCA，
∴40°+x=80°-x，解得x=20°，
∴∠OCA=80°-x=80°-20°=60°．
故答案为40°，60°．
互助这道作业题的同学还参与了下面的作业题
题1： 如图,三角形ABC内接于圆O,连接OA,OC.若AB=AC,弧BC为100度,求角AOC和弧AC的度数[数学科目]
连接AO
因为AB=AC；BO=OC；AO=AO
所以,三角型AOB全等于三角型AOC
所以,角AOB=角AOC
所以角AOC=（360-100）/2=130度
所以弧AC的度数是130度(劣弧)或230度（优弧）
题2： 移动OA怎么使用?好像现在有OA可以安装在智能手机上了,这就现在流行的移动OA吗?要怎么使用阿?
是的,对于很多公司来说,或者说对于经常出差的朋友们来说,虽然用OA办公很快捷,但是却不是特别方便,遇到没有网络活急着要登录OA办公的时候就更郁闷了.所以,伟峰两年前就开始研发移动OA,也就是手机OA,现在伟峰科技的移动OA办公系统现在比较成熟,移动OA办公系统现在来说实现的功能没有PC机上的全面.但移动OA不仅能够轻松安装在IPHONE、平板电脑上,只要是智能手机都可以安装,没有手机型号的限制,现在很多公司的移动OA都有手机型号这方面的限制……伟峰OA真正实现了所谓的“移动办公”~!
经常要出差的朋友可以试用一下,触控操作很不错,设计也很人性化.总是,以后出差在外,或者在公交车和地铁上也能够轻轻松松的办公审批报表、文件了.搜索一下伟峰OA到我们官网了解一下吧.
题3： 【若OA平分角BAC角OBC=角OCB求证三角形ABC为等腰三角形快】[数学科目]
过点O作OD垂直于AB于D
过点O作OE垂直于AC于E
再证Rt△AOD全等于Rt△AOE（AAS）
得出OD=OE
就可以再证Rt△DOB全等于Rt△EOC（HL）
得出∠ABO＝∠ACO
再因为角OBC=角OCB
得出∠ABC＝∠ABC
得出等腰△ABC
题4： 【如图，∠AOB=90°，OM平分∠AOB，将直角三角板的顶点P在射线OM上移动，两直角边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．】[数学科目]
PC与PD相等．理由如下：过点P作PE⊥OA于点E，PF⊥OB于点F．∵OM平分∠AOB，点P在OM上，PE⊥OA，PF⊥OB，∴PE=PF（角平分线上的点到角两边的距离相等）又∵∠AOB=90°，∠PEO=∠PFO=90°，∴四边形OEPF为矩形，∴∠EP...
题5： 如图，四边形AOCB是直角梯形，AB∥OC，OA=10，AB=9，∠OCB=45°，求点A，B，C的坐标及直角梯形AOCB的面积．[数学科目]
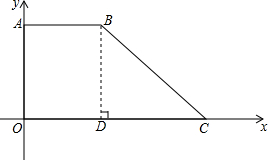过点B作BD⊥CO于点D，
∵∠OCB=45°，AB∥OC，OA=10，AB=9，
∴BD=CD=10，OD=9，
∴CO=OD+DC=9+10=19，
故A点坐标为：（0，10），
B点坐标为：（9，10），
C点坐标为：（19，0），
直角梯形AOCB的面积为：12