【如图三角形abc】如图在三角形abc中ab=ac如图在△ABC中,AB=AC,D是AB上..._数学_wchesqm
编辑: admin 2017-15-06
-
4
DE=2EF
证明:过点D作DG‖AE,交BF于G
∵AB=AC(已知)
∴∠B=∠ACB(等边对等角)
∵DG‖AE
∴∠DGB=∠ACB(两直线平行,同位角相等)
∠CEF=∠GDF(两直线平行,内错角相等)
∴∠B=∠DGB(等量代换)
∴BD=DG(等角对等边)
∵CE=BD(已知)
∴CE=DG(等量代换)
在⊿CFE和⊿GFD中,
∠CFE=∠GFD(对顶角相等)
∠CEF=∠GDF
CE=DG
∴⊿CFE≌⊿GFD(AAS)
∴EF=DF
∵DE=EF+DF
∴DE=2EF
过程看起来有点麻烦,但是很详细了.括号里的字是帮助你理解的,可以不写.
尽量用数学语言打出来……应该能看懂吧.
其他同学给出的参考思路:
DE=2EF
证明:过点D作DG‖AE,交BF于G
∵AB=AC(已知)
∴∠B=∠ACB(等边对等角)
∵DG‖AE
∴∠DGB=∠ACB(两直线平行,同位角相等)
∠CEF=∠GDF(两直线平行,内错角相等)
∴∠B=∠DGB(等量代换)
∴BD=DG(等角对等边)
∵CE=BD(已知)
∴CE=DG(等量代换...
展开
互助这道作业题的同学还参与了下面的作业题
题1: 如图1,在三角形ABC中,角BAC=90度,AB=AC,直线m经过点A,BD垂直于直线m,垂足分别为点D,E.求证:DE=BD+CE如图2,将1中的条件改为:在三角形ABC中,AB=AC,D,A,E三点都在直线m上,并且有角BDA=角AEC=角BAC=α,其中α[数学科目]
(1)证明:因为AB=AC,且∠BDA=∠BAC=∠AEC,
又∠DBA+∠DAB+∠BDA=180,
∠EAC+∠ECA+∠AEC=180
∠DAB+∠EAC=180
所以有 ∠DBA=∠EAC,∠DAB=∠ECA
根据AB=AC可得 三角形 ADB全等于三角形 CEA
所以有 BD=AE,DA=EC
所以DE=BD+ CE
证明完毕
(2)结论DE=BD+ CE是成立的,因为(1)中的证明与α角的大小无关,所以(1)的证明过程
对于(2)同样适用.
题2: 【如图,在三角形abc中,ab=ac=10,S三角形abc=30,求bc的长】[数学科目]
两边相等说明其为等腰三角形,左右角度均为x.过a点作bc垂线,交bc于e,则ae为高.所以S=1/2*10sinx*2*10cosx=30,得出sin2x=0.6,再求bc=2*10cosx即可,角度不是正常角度,不过相信用计算器可以算出答案约为19,自己再做做.
题3: 【如图,已知△ABC中,AB=10,BC=9,AC=17.求BC边的高.】[数学科目]
延长CB,作AD⊥CB延长线与D点,设AD=x,BD=y,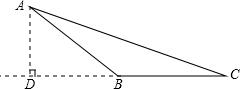 在直角△ADB中,AB2=x2+y2,
在直角△ADB中,AB2=x2+y2,
在直角△ADC中,AC2=x2+(y+BC)2,
解方程得 y=6,x=8,
即AD=8,∵AD即BC边上的高,
∴BC边上的高为8.
答:BC边上的高为 8.
题4: 【如图,在三角形ABC中,已知AB=AC=20,角ABC=15度,CD是腰AB上的高,求CD的长】[数学科目]
你要想到:角CAD是△ABC的外角
△ABC是等腰三角形.∠ABC=∠ACB=15°
所以∠CAD=30°.
斜边AC=20.CD是斜边所对的直角边等于斜边的一半
CD=10
题5: 如图,三角形abc中,ab=4,ac=5
过E点作EG⊥BA于G点.角平分线得AF=AG,EG=EF,得△EBG≌△ECA,得CF=BG,CF=CA-AF,BG=BA+AF,解得AF=0.5
