【已知如图ad平行bc】【如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相..._数学_凡丈
编辑： admin 2017-15-06
-
4
证明：在AB上截取AF=AD，
∵AE平分∠PAB，
∴∠DAE=∠FAE，
在△DAE和△FAE中，
∵AD＝AF∠DAE＝∠FAEAE＝AE
∴△DAE≌△FAE（SAS），
∴∠AFE=∠ADE，
∵AD∥BC，
∴∠ADE+∠C=180°，
∵∠AFE+∠EFB=180°，
∴∠EFB=∠C，
∵BE平分∠ABC，
∴∠EBF=∠EBC，
在△BEF和△BEC中，
∵∠EFB＝∠C∠EBF＝∠EBCBE＝BE，
∴△BEF≌△BEC（AAS），
∴BC=BF，
∴AD+BC=AF+BF=AB．
其他同学给出的参考思路：
（1）证明：延长AE交BC的延长线于M，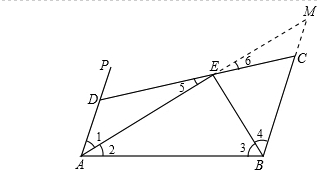
∵AE平分∠PAB，BE平分∠CBA，
∴∠1=∠2，∠3=∠4，
∵AD∥BC
∴∠1=∠M=∠2，∠1+∠2+∠3+∠4=180°
∴BM=BA，∠3+∠2=90°，
∴BE⊥AM，
在△ABE和△MBE中，∠3=∠4BE=BE∠AEB=∠MEB
∴△ABE≌△MBE
∴AE=ME，
在△ADE和△MCE中，∠1=∠MAE=ME∠5=∠6；
∴△ADE≌△MCE，
∴AD=CM，
∴AB=BM=BC+AD．
互助这道作业题的同学还参与了下面的作业题
题1： 如图,AP平行于BC,∠PAB的平分线与∠CBA的平分线交于点E,CE的延长线交AP于点D（1）说明：AB=AD+BC（2）若BE=3,AE=4,求四边形ABCD的面积[数学科目]
（1）在AB上截取AF=AD,连结EF,则
∵AE平分∠PAB
∴由边角边可得△ADE≌△AFE
∴∠EFA=∠ADE
∵AP‖BC
∴∠BCD+∠ADE=180°
又∠AFE+∠EFB=180°
∴∠BCD=∠BFE=180°
又∵BE平分∠CBA
∴由角角边可得△BCE≌△BFE
∴BF=BC
∴AB=AF+BF=AD+BC
(2)延长AE交BC的延长线于M,则△AED≌△MEC
∴四边形ABCD的面积=△ABM的面积=8×3/2=12
题2： 如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．[数学科目]
证明：在AB上截取AF=AD，
∵AE平分∠PAB，
∴∠DAE=∠FAE，
在△DAE和△FAE中，
∵AD＝AF∠DAE＝∠FAEAE＝AE
∴△DAE≌△FAE（SAS），
∴∠AFE=∠ADE，
∵AD∥BC，
∴∠ADE+∠C=180°，
∵∠AFE+∠EFB=180°，
∴∠EFB=∠C，
∵BE平分∠ABC，
∴∠EBF=∠EBC，
在△BEF和△BEC中，
∵∠EFB＝∠C∠EBF＝∠EBCBE＝BE，
∴△BEF≌△BEC（AAS），
∴BC=BF，
∴AD+BC=AF+BF=AB．
题3： 【如图,AD//BC,角PAB的平分线与角CBA的平分线相交于点E,CE的延长线交AP于D,求证AD十BC=AB】[数学科目]
题4： 如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．[数学科目]
证明：在AB上截取AF=AD，
∵AE平分∠PAB，
∴∠DAE=∠FAE，
在△DAE和△FAE中，
∵AD＝AF∠DAE＝∠FAEAE＝AE
∴△DAE≌△FAE（SAS），
∴∠AFE=∠ADE，
∵AD∥BC，
∴∠ADE+∠C=180°，
∵∠AFE+∠EFB=180°，
∴∠EFB=∠C，
∵BE平分∠ABC，
∴∠EBF=∠EBC，
在△BEF和△BEC中，
∵∠EFB＝∠C∠EBF＝∠EBCBE＝BE，
∴△BEF≌△BEC（AAS），
∴BC=BF，
∴AD+BC=AF+BF=AB．
题5： 【已知如图ap平行于bc角pab的平分线与角cba的平分线交与点ece的连线交ap于d求证已知如图ap平行于bc角pab的平分线与角cba的平分线交与点ece的连线交ap于d求证ad+bc=ab】[数学科目]
证明：在AB上截取AF=AD,连接EF
因为角PAB和角CAB的平分线交于点E
所以角DAE=角FAE=1/2角BAD
角EBC=角EBF=1/2角ABC
因为AE=AE
所以三角形ADE和三角形AFE全等（SAS)
所以角AED=角AEF
因为AD平行BC
所以角BAD+角ABC=180度
所以角FAE+角EBF=90度
因为角FAE+角EBF+角AEB=180度
所以角AEB=90度
因为角AEB+角ADE+角CEB=180度
所以角ADE+角CEB=90度
因为角AEB=角AEF+角BEF=90度
所以角BEF=角CEB
因为BE=BE
角EBC=角EBF（已证）
所以三角形CBE和三角形FBE全等（ASA)
所以BC=BF
因为AB=AF+BF
所以AD+BC=AB