【如图在rt△abc中】如图，在Rt△ABC中，∠C=90°，∠A的平分线交BC于点E，EF..._数学_213验证码9

编辑： admin           2017-15-06         

互助这道作业题的同学还参与了下面的作业题

题1： 如图在Rt△ABC中AB⊥ACAD⊥BCBE平分∠ABC交AD于点EEF‖AC下列结论中成立的是AAB=BFBAE=EDCAD=DCD∠ABE=∠DFED也能可以阿--不用30度吧用角的等量代换就可以了

选A AB=BF

证明：

∵∠BAC=90°,AD⊥BC

∴∠BAD+∠ABC=∠C+∠ABC=90°

∴∠BAD=∠C

∵EF‖AC

∴∠C=∠EFB

∴∠EFB=∠EAB

∵∠ABE=∠FBE,BE=BE

∴△ABE≌△BFE

∴AB=BF

D不可以,除非∠C=30度才行

不是啊,∠BFE=∠C=∠BAE,但不能确定等于∠ABE哦!

题2： 【问一个数学题,如图,在RT△ABC中,角A=90度,AB=3,AC=4第一问,如图①,四边形DEFG为△ABC的内接正方形,求正方形的边长第二位,如图②,△ABC内有并排的两个相等的正方形,且它们组成的矩形内接于△ABC,】[数学科目]

第一问:

作AM垂直于BC,且交GF于N.

在RT△ABC中,角A=90度,AB=3,AC=4,所以BC=5(勾股定理).

AM为△ABC斜边上的高,所以AM=12/5.

设正方形边长为X,则MN=GF=X

因为角A=角A,GF平行于BC得到角AGF等于角B,所以△ABC相似于△AGF.

所以:AN比AM=GF比BC,又因为AN=12/5-X

所以:(12/5-X):12/5=X:5,解得X=60/37

第二问:

作AM垂直于BC,且交GF于N.

设正方形边长为X,则MN=X,GF=2X

同第一问利用相似,可得:(12/5-X):12/5=2X:5,解得X=60/49

第三问:

作AM垂直于BC,且交GF于N.

设正方形边长为X,则MN=X,GF=3X

同第一问利用相似,可得:(12/5-X):12/5=3X:5,解得X=60/61

第四问:

由第一二三问知边长的分子总为60,分母在改变,

找规律知分母为:12n+25

所以第N个正方形边为:60/12n+25

题3： 已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．（1）当∠EDF绕D点旋转到DE⊥AC于E时（如图1），易证S△DEF+S△CEF=12S[数学科目]

（1）显然△AED，△DEF，△ECF，△BDF都为等腰直角三角形，且全等，
则S_△DEF+S_△CEF=12

S_△ABC；
（2）图2成立；图3不成立．
图2证明：过点D作DM⊥AC，DN⊥BC，则∠DME=∠DNF=∠MDN=90°，
又∵∠C=90°，
∴DM∥BC，DN∥AC，
∵D为AB边的中点，
由中位线定理可知：DN=12
AC，MD=12
BC，
∵AC=BC，
∴MD=ND，
∵∠EDF=90°，
∴∠MDE+∠EDN=90°，∠NDF+∠EDN=90°，
∴∠MDE=∠NDF，
在△DME与△DNF中，
∵∠DME＝∠DNFMD＝ND∠MDE＝∠NDF
，
∴△DME≌△DNF（ASA），
∴S_△DME=S_△DNF，
∴S_{四边形DMCN}=S_{四边形DECF}=S_△DEF+S_△CEF，
由以上可知S_{四边形DMCN}=12
S_△ABC，
∴S_△DEF+S_△CEF=12
S_△ABC．
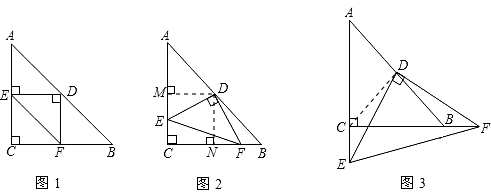
图3不成立，连接DC，
证明：△DEC≌△DBF（ASA，∠DCE=∠DBF=135°）
∴S_△DEF=S_{五边形DBFEC}，
=S_△CFE+S_△DBC，
=S_△CFE+

S

△ABC
2
，
∴S_△DEF-S_△CFE=

S

△ABC
2
．
故S_△DEF、S_△CEF、S_△ABC的关系是：S_△DEF-S_△CEF=12
S_△ABC．

题4： 如图,在rt三角形ABC中,角C=90°,角A=60°,点E,F分别在AB,AC上,把角A沿着EF对折,使点A落在BC上点D处,且使ED垂直于BC1.猜测AE与BE的数量关系,并说明理由2.求证：四边形AEDF是菱形

⑴∵∠A=60在,∴∠B=30°,

在RTΔBDE中,DE=1/2BE,

则折叠知,AE=DE,

∴AE=1/2BE(或BE=2AE).

⑵由折叠知：∠FEA=∠FED,

∵DE⊥BC,∠C=90°,

∴DE∥AC,∴∠FED=∠EFA,

∴∠FEA=∠EFA,∴AE=AF,

∴AF=DE,

∴四边形AEDF是平行四边形(AF与DE平行且相等),

又AE=AF,

∴平行四边形AEDF是菱形.

题5： 【如图,AD是Rt△ABC斜边上的高,BE平分∠B交AD于G,交AC于E,过E作EF⊥BC于F.试证明：1,AG=AE;2,四边形AEFG是菱形.这个题,希望能尽量规范.】[数学科目]

1.∵∠C+DAC=90°,∠BAD+∠DAC=90°

∴∠C=∠BAD

∵BE平分∠ABC

∴∠ABE=∠CBE

∵∠AGE=∠BAD+∠ABE,∠AEG=∠C+∠CBE

∴∠AGE=∠AEG

∴AG=AE

2.∵BE平分∠ABC,EF⊥BC,EA⊥AB

∴EA=EF=AG

∵AD⊥BC,EF⊥BC

∴AD//EF

∵AG=EF

∴AGFE是平行四边形,

因为AG=AE

∴四边形AEFG是菱形

•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克