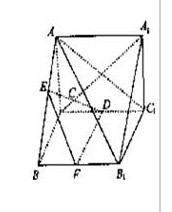
【de平行于面ab1c】...B1C1中,若D是棱CC1的中点,棱AB的中点为E,证明DE平行于平面AB1C..._数学
编辑: admin 2017-15-06
-
4
取BB1的中点为F,连接DF、EF
则可证平面AB1C1平行平面DEF,所以DE平行于平面AB1C1
互助这道作业题的同学还参与了下面的作业题
题1: 在三棱柱ABC—A1B1C1中,D是AB的中点,求证:AC1‖面CDB1[数学科目]
取A1B1中点D1.连C1D1,AD1.因CD‖C1D1,AD1‖DB1.所以面AC1D1‖面CDB1.得AC1‖CDB1
题2: 如图三棱柱ABC~A1B1C1的侧棱AA1垂直底面ABC,∠ABC=90°,E是棱CC1上的动点,F是AB中点,AC=1,BC=2,AA1=4.求,1,当E是棱CC1中点时,求证CF∥平面AEB1.2,在棱CC1上是否存在点E,使得二面角A—EB1—B的余弦值是17分之2[数学科目]
1.设AB1中点为G.连接各点.由AA1⊥底面ABC知此为直三棱柱.
由G为AB1中点,F为AB中点,得GF∥BB1且GF=1/2BB1.
由E为CC1中点,CE∥BB1且CE=1/2CC1=1/2BB1.
故GF∥CE且GF=CE,四边形GFCE为平行四边形.
故GE∥CF,CF∥平面AEB1.
2.以B为原点,BA为x轴,BC为y轴,BB1为z轴建立空间直角坐标系.设E(0,2,λ).
故A(1,0,0),B1(0,0,4),AE=(-1,2,λ),AB1=(-1,0,4)
由AA1垂直底面ABC得AA1⊥AB,BB1⊥AB,由∠ABC=90°知AB⊥BC,
故AB⊥平面BB1C1C,平面BB1E即平面BB1C1C法向量取BA=(1,0,0).
设平面AEB1的法向量a=(x,y,z),则a·AE=0,a·AB1=0
解得(λ-4)z=-2y,取z=-2,则y=λ-4,x=-8,即a=(-8,λ-4,-2).
由二面角A-EB1-B余弦值2√17/17得
2√17/17=cosθ=|cos|=|a·BA|/|a||BA|=8/√[64+4+(λ-4)2]
解得λ=4±2√51.
验证知均不在CC1上,故不存在.
(楼主是不是打错题了?)
题3: 直三棱柱abc—a1b1c1中,ab垂直于ac,d、e分别为aa1、b1c的中点,de垂直于平面bcc1,问1:证明AB=AC[数学科目]
作BC中点F,连结AF,EF.E,F分别是B1C,BC的中点,易证DE与AF平行且相等.则AF⊥平面BCC1B1,则AF⊥BC,又由于F是BC中点.从而可知这一定是一个等腰三角形,即AB=AC
题4: 在直三棱柱ABC-A1B1C1中,角ACB=90°,AB=2,BC=1,AA1=根号6,D是棱CC1的中点,证明:A1D⊥平面AB1C1求二面角B-AB1-C1[数学科目]
第一个问题:令AD与AC1的交点为E.∵∠ACB=90°、BC=1、AB=2,∴∠BAC=30°,∴AC=√3.∵ABC-AB1C1是直三棱柱,∴∠CC1A1=∠AA1C1=90°、CC1=AA1=√6、A1C1=AC=√3,又CD=C1D,∴C1D=CC1/2=√6/2.∴tan∠A1...
题5: 如图所示,在三棱柱ABC—A1B1C1中,A1A⊥平面ABC,AB=2BC,AC=AA1=3^1/2BC,证明A1⊥AB1C1若D是棱DD1的中点,在棱AB上是否存在一点E,使DE∥AB1C1?若存在请确定点E的位置,若不存在,请说明理由。大侠[数学科目]
证明:(1)∵AB=2BC,AC= BC,
∴△ABC为直角三角形,且∠ACB= .
从而BC⊥AC.又AA1⊥平面ABC,
∴AA1⊥BC,∴BC⊥CC1(2分)
从而BC⊥面ACC1A1,∴BC⊥A1C,
则B1C1⊥A1C(4分)∵AC=AA1∴侧面ACC1A1为正方形,∴AC1⊥A1C.
又B1C1∩AC1=C1,∴ C⊥面AB1C1(6分)
(2)存在点E,且E为AB的中点((8分))
下面给出证明:
取BB1的中点F,连接DF,则DF∥B1C1.
∵AB的中点为E,连接EF,则EF∥AB1.B1C1与AB1是相交直线,∴面DEF∥面AB1C1.(10分)
而DE?面DEF,∴DE∥面AB1C1(12分)
by 巴蜀蕉叶击雨泪