【△abc中点de】三角形ABC，BD和CE是高，M是BC的中点，P是DE的中点，求证PM垂直DE_数学_3453459
编辑： admin 2017-15-06
-
4
我来
互助这道作业题的同学还参与了下面的作业题
题1： 已知:如图,△ABC中,BD和CE是高,M为BC的中点,P为DE的中点.求证:PM⊥DE.如题,如图.[数学科目]
证明：联结EM、DM,则EM=1/2BC,DM=1/2BC
故EM＝DM
又P为DE的中点,所以PM⊥DE.
题2： 三角形ABC中BD,CE平分角B,角C,P为ED中点,PH垂直BC,PM垂直AB,PN垂直AC求证:PH=PM+PN
过E做ED⊥BC,DK⊥BC,EF‖PH‖DK在梯形EFKD中P为中点,所以H为MN中点PH=1/2（EF+DK）在做EG⊥AC,则EG=EF在△EGD中,可证PN是中位线PN=1/2EG过D做DO⊥AB在△ODE中可证PM是中位线OD=DKPM=1/2ODPM+PN =1/2OD+1/2EG=1/2（EF...
题3： 如图,△ABC中,BD和CE是高,M为BC的中点,P为DE的中点,求证：PM垂直于DE.[数学科目]
证明：联结EM、DM,则EM=1/2BC,DM=1/2BC
故EM＝DM
又P为DE的中点,所以PM⊥DE.
题4： 【如图，已知BD、CE分别是△ABC的AC、BC边上的高，G、F分别是BC、DE的中点．求证：GF⊥DE．】[数学科目]
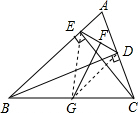证明：如图，连接EG、DG，
∵BD、CE分别是△ABC的AC、BC边上的高，点G是BC的中点，
∴DG=EG=12
∵点F是DE的中点，
∴GF⊥DE．
题5： 三角形ABC；BD平分角B交AC于D；CE平分角C交AB于E；DE中点Q分别垂直AB;BC;CA于MQN；求PQ=PM+PN[数学科目]
如图,过E作BC,AC的垂线EJ,ET；过D作CB,CA的垂线DK,DL.则
PM=1/2 DL=1/2 DK,PN=1/2 ET=1/2EJ.
而PQ=1/2 (EJ+DK)=PM+PN
