【如图A在de上】【如图，点A在DE上，AC=CE，∠1=∠2=∠3，则DE的长等于()..._数学_kmuhqz
编辑： admin 2017-15-06
-
4
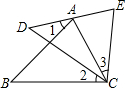∵∠2=∠3，
∴∠DCE=∠3+∠ACD=∠2+∠ACD=∠ACB，
即：∠ACB=∠DCE，
又∵AC=CE，
∴∠E=∠CAE，
∠1+∠BAC=∠DAC=∠3+∠CEA，
∵∠1=∠3，
∴∠BAC=∠CEA
在△ABC和△EDC中，
∠ACB=∠DCE，AC=CE，∠BAC=∠E，
∴△ABC≌△EDC，
∴DE=AB．
故选C．
其他同学给出的参考思路：
DE＝AB
证明：
∵∠CAD＝∠BAC+∠1, ∠CAD＝∠E+∠3
∴∠BAC+∠1＝∠E+∠3
∵∠1＝∠3
∴∠BAC＝∠E
∵∠ACB＝∠2+∠ACD，∠ECD＝∠3+∠ACD，∠2＝∠3
∴∠ACB＝∠ECD
∵AC＝CE
∴△ABC≌△EDC （ASA）
∴DE＝AB
明...
展开
互助这道作业题的同学还参与了下面的作业题
题1： 【如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于（）.】[数学科目]
∵∠ACB＝∠ACD+∠2, ∠ECD＝∠ACD+∠3, ∠2＝∠3
∴∠ACB＝∠ECD
∵∠CAD＝∠1+∠CAB,∠CAD＝∠3+∠E,∠1＝∠3
∴∠CAB＝∠E
∵AC＝CE
∴△CAB≌△CED （ASA）
∴DE＝AB
数学辅导团解答了你的提问,理解请及时采纳为最佳答案.
题2： 如图，△ABC中，AB=AC，点D、E分别在AB、AC的延长线上，且BD=CE，DE与BC相交于点F．求证：DF=EF．[数学科目]
证明：过D点作DG∥AE交BC于G点，如图，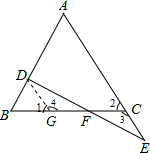
∴∠1=∠2，∠4=∠3，
∵AB=AC，
∴∠B=∠2，
∴∠B=∠1，
∴DB=DG，
而BD=CE，
∴DG=CE，
在△DFG和△EFC中
∠4＝∠3∠DFG＝∠EFCDG＝CE
∴△DFG≌△EFC，
∴DF=EF．
题3： 【如图，△ABC中，AB=AC，点D、E分别在AB、AC的延长线上，且BD=CE，DE与BC相交于点F．求证：DF=EF．】[数学科目]
证明：过D点作DG∥AE交BC于G点，如图，
∴∠1=∠2，∠4=∠3，
∵AB=AC，
∴∠B=∠2，
∴∠B=∠1，
∴DB=DG，
而BD=CE，
∴DG=CE，
在△DFG和△EFC中
∠4＝∠3∠DFG＝∠EFCDG＝CE
∴△DFG≌△EFC，
∴DF=EF．
题4： 【如图，已知∠B+∠D=180°，AE、BD相交于点C，AC=CE，求证：AB=DE．】[数学科目]
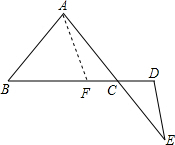证明：如图，过A点作AF∥DE交BC于F，
∴∠CAF=∠CED，∠CFA=∠CDE，
又∵AC=CE，
∴△ACF≌△EDC，
∴∠D=∠AFC，AF=DE，
∵∠B+∠D=180°，∠AFC+∠AFB=180°，
∴∠B=∠AFB，
∴AB=AF，
∴AB=DE．
题5： 【如图，在等腰梯形ABCD中，AB∥CD，延长底边AB到E，使得BE=DC．求证：AC=CE．】[数学科目]
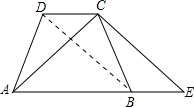证明：连接BD．
∵AB∥CD，BE=DC，
∴四边形BECD是平行四边形，
∴CE=BD，
∵四边形ABCD是等腰梯形，
∴AC=BD，
∴AC=CE．