【从三角形的三】怎样证明从三角形重心连接三个顶点组成的三个三角形面积相等_数学_孤傲淽柦挅
编辑: admin 2017-15-06
-
4
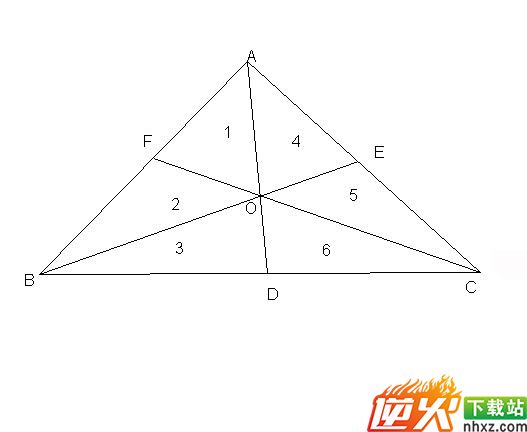
如图:O是重心,
首先要说明的一点是,1、三角形的面积=边和边到顶点距离乘积的1/2
2、重点是三角形各边中线的交点
3、由于O点是三角形1和2的共同顶点,所以O点到AB间的高应该是三角形1和2的AF和BF上的高,即同顶点上三角形底边上的高是相同的
证明:由于AF=BF,所以S1=S2(底边上的高相同),S1+S4+S5=S2+S3+S6;因而得S3+S6=S4+S5
又因AE=EC,所以S4=S5,同样可得S1+S2=S3+S6
故:S1+S2=S3+S6=S4+S5
其他同学给出的参考思路:
设G是△ABC的重心,连AG并延长交BC于D,显然有:BD=CD[△的重心是其中线的交点]。
△GAD的面积=△GCD的面积,△ABD的面积=△ACD的面积,得:
△ABD的面积-△GAD的面积=△ACD的面积-△GCD的面积。
而△GAB的面积=△ABD的面积-△GAD的面积,
△GAC的面积=△ACD的面积-△GCD的面积。
于是:△GAB的面积=△G...
展开
互助这道作业题的同学还参与了下面的作业题
题1: 【向量法证明三角形重心与顶点连线的三个三角形的面积比必须向量法.有图的加分,不二话】
设:△ABC,重心为G,作CD‖BG,BD‖CG,GD,BC相交于O,
则BDCG为平行四边形,BO=CO,GO=DO,向量GB+向量GC=向量GD=2向量GO
又∵向量GB+向量GC=-向量GA (∵G为重心)
∴向量GA=-2向量GO,∴A,G,O三点共线,|AG|=2|GO|
∴S△AGC=2S△GOC,S△AGB=2S△GOB,
又S△GOC=S△GOB,∴S△AGC=S△AGB=S△BGC
∴三角形重心与顶点连线的三个三角形的面积比=1:1:1
题2: 如何求证:重心和三角形3个顶点组成的3个三角形面积相等只要思路即可[数学科目]
重心是三角形三条中线的交点,到顶点的距离为到对边中点的2 倍,它也是三条中线的三等分点.
题3: 【证明三角形的重心与其三个顶点的连线的向量之和为零向量】[数学科目]
设,三顶点A(x1,y1),B(x2,y2),C(x3,y3)
则重心O[(x1+x2+x3)/3,(y1+y2+y3)/3]
向量OA=[x1-(x1+x2+x3)/3,y1-(y1+y2+y3)/3]
向量OB=[x2-(x1+x2+x3)/3,y2-(y1+y2+y3)/3]
向量OC=[x3-(x1+x2+x3)/3,y3-(y1+y2+y3)/3]
则,向量OA+向量OB+向量OC
=[x1-(x1+x2+x3)/3,y1-(y1+y2+y3)/3]+[x2-(x1+x2+x3)/3,y2-(y1+y2+y3)/3]+[x3-(x1+x2+x3)/3,y3-(y1+y2+y3)/3]
=(0,0)
即得证
题4: 【如何证明重心是到三角形三顶点的距离的平方和最小的点?】[数学科目]
设三角形三个顶点为(x1,y1),(x2,y2),(x3,y3) 平面上任意一点为(x,y) 则该点到三顶点距离平方和为:(x1-x)^2+(y1-y)^2+(x2-x)^2+(y2-y)^2+(x3-x)^2+(y3-y)^2 =3x^2-2x(x1+x2+x3)+3y^2-2y(y1+y2+y3)+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2=3(x-1/3*(x1+x2+x3))^2+3(y-1/3(y1+y2+y3))^2+x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2 显然当x=(x1+x2+x3)/3,y=(y1+y2+y3)/3(重心坐标)时上式取得最小值为 x1^2+x2^2+x3^2+y1^2+y2^2+y3^2-1/3(x1+x2+x3)^2-1/3(y1+y2+y3)^2 证毕
题5: 如何证明三角形重心到顶点的距离与重心到对边中点的距离之比为2:1
已知:在△ABC中,AD、BE、CF分别是AB、BC、CA边上的中线
求证:(1)AD、BE、CF相交于一点O
(2)AO:OD=BO:OE=CO:OF=2:1
证明:设AD和BE相交于O'
延长O'D到G,使DG=O'D,连接BG
∵BD=DC,O'D=DG
∴BGCO'是平行四边形,∴BE‖CG
在△AGC中,
∵E是AC的中点,EO'‖CG,
∴EO'平分AG,即AO'=O'G
∴AO':O'D=2:1
同理,CF与AD的交点O"也满足AO":O"D=2:1
故O'与O"重合,设为O,即AD、BE、CF相交于一点O
同理可证BO:OE=CO:OF=2:1
证毕.
