【比赛过程中有一名选】求答案及过程从5名学生中选出3人参加演讲比赛，其中有..._数学_笑插鸿蒙亲吗88

编辑： admin           2017-15-06         

互助这道作业题的同学还参与了下面的作业题

题1： 从6名学生和4名教师中选出3人参加演讲比赛,选出的3人中恰好有1名学生的选法有几种[数学科目]

4名教师中选两名,共6种选法

再6种选法分别搭配1名学生 6*6=36

题2： 从6名学生和4名教师中选出3人参加演讲比赛,选出的3人中至少有一名学生的选法有几种[数学科目]






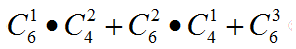
答案我懒得算了……式子应该就是这么列.

题3： 【从6名学生和4名教师中选出3人参加演讲比赛选出3人中至少一名学生的选法】[数学科目]

没法打数学符号,就简易说一下,不用排列组合了：

从10人中选3人（无顺序）：10×9×8÷3÷2=120种方法；

这三人中没有一个学生：4种方法；

所以,选出的三人中至少有一名学生：120-4=116种方法.

题4： 从5名女同学和4名男同学中选出4人参加四场不同的演讲，分别按下列要求，各有多少种不同选法？（1）男、女同学各2名；（2）男、女同学分别至少有1名；（3）在（2）的前提下，男同学甲[数学科目]

（1）男、女同学各2名的选法有C₄²×C₅²=6×10=60种，故总的不同选法有60×A₄⁴=1440种；
即男女同学各两名的选法共有1440种．
（2）“男、女同学分别至少有1名”包括有“一男三女”，“二男二女”，“三男一女”，故选人种数为C₄¹×C₅³+C₄²×C₅²+C₄³×C₅¹=40+60+20=120
故总的安排方法有120×A₄⁴=2880
故不同的选法有2880种．
（3）可计算男同学甲与女同学乙同时选出的种数，由于已有两人，故再选两人即可，此两人可能是两男，一男一女，两女，故总的选法有C₃²+C₄¹×C₃¹+C₄²=21
故总的选法有2880-21×A₄⁴=2376
故不同的选法种数是2376种

题5： 【从4名男生和2名女生中任选3人参加演讲比赛,1.求所选3人都是男生的概率2.求所选人中恰有一名女生的概率3.求所选3人中至少有一名女生的概率不要C什么的，没有学就是画图算概率的呢中，】[数学科目]

设4名男生分别为A,B,C,D,2名女生分别为E,F

抽取情况有（A,B,C）（A,B,D)(A,B,E)(A,B,F)(A,C,D)(A,C,E)(A,C,F)(A,D,E)(A,D,F)(A,E,F)(B,C,D)(B,C,E)(B,C,F)(B,D,E)(B,D,F)(B,E,F)

(C,D,E)(C,D,F)(C,E,F)

(D,E,F)20种情况

(1)所选3人都是男生的情况有4种,所以P=4/20=1/5

(2)所选人中恰有一名女生的情况有12种,所以P=12/20=3/5

•   4
  

相关文章

一公分等于几厘米

一吨等于多少立方米

消费税计算公式

立方米和吨的换算

函数的值域

10公分等于多少厘米

1公斤等于多少千克

数学的由来

一元一次方程计算题

金条多少克