【已知圆o的半径为6】如图，已知圆O的半径为6cm，射线PM经过点O如图，已知⊙O..._数学_dlxtghza
编辑： admin 2017-15-06
-
4
1.连OQ
OQ=R=6cm
OP=10cm
∴PQ=8cm
2.设t1s时AB第一次切⊙O于C
连OA、OC
∵PA:PB=4t:5t=4:5=PQ:PO
∴△PAB∽△POQ
又AC、AQ都与⊙O相切
易证ACOQ是正方形
∴PA=8-6=2=4t1
t1=0.5s
设t2s时AB第二次切⊙O于C'
连OC'
同理可证OC'BQ是正方形
PB=4t2=8+6=14
t2=3.5 s
其他同学给出的参考思路：
1)连接OQ，PQ与圆O相切，故OQ垂直于PQ
所以PQ^2=PO^2-OQ^2,即PQ^2=10^2-6^2=64,PQ=8(cm)
2)设t秒时直线与圆O相切于E，如图，则PB：PA=4：5；又PQ：
PO=8cm:10cm=4:5.故PQ：PO=PB:PA,又∠P=∠P
∴⊿PBA∽⊿PQO，则∠PBA=∠PQO=90度；又∠PQO=∠BEO=90度；...
展开
互助这道作业题的同学还参与了下面的作业题
题1： 如图,圆O的半径为6cm,射线PM过点O,OP=10cm,射线PN与圆O相切于点Q,A、B两点同时从点P出发,如图,圆O的半径为6cm,射线PM过点O,OP=10cm,射线PN与圆O相切于点Q,A、B两点同时从点P出发,点A以5cm/s的速度沿射[数学科目]
1)连接OQ,PQ与圆O相切,故OQ垂直于PQ
所以PQ^2=PO^2-OQ^2,即PQ^2=10^2-6^2=64,PQ=8(cm)
2)设t秒时直线与圆O相切于E,如图,则PB：PA=4：5；又PQ：
PO=8cm:10cm=4:5.故PQ：PO=PB:PA,又∠P=∠P
∴⊿PBA∽⊿PQO,则∠PBA=∠PQO=90度；又∠PQO=∠BEO=90度；
OQ=OE,故四边形BQOE为正方形,BQ=QO=6,PB=4t=2,t=1/2.
所以当t=1/2s时,直线AB与圆相切.
题2： 如图,直线AB、CD相交于点O,∠AOC＝30°,半径为1cm的圆P的圆心在射线OA上,开始时,PO＝6cm.如果圆P以1cm/秒的速度沿由A向B的方向移动,那么当圆P的运动时间t（秒）满足何条件时,圆P与直线CD相离、相[数学科目]
你那个PO=6cm中的P是否是圆心!
下面是以P点为圆心的做法!
首先我们找到临界点,即相切
当PO=2时,圆与直线CD相切
即t=4这只是左边,我们还要考虑右边,右边也是一样的,t=PO 2=8
即
相切t=4或t=8
相离t＜4或t＞8
相交4＜t＜8
因为是手机上的,所以没附图!也讲不详细!
仅供参考,因为我也好久没接触数学了!
题3： 【如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q．A,B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动．设运动时间为ts．（1）求PQ的】[数学科目]
1.连OQ
OQ=R=6cm
OP=10cm
∴PQ=8cm
2.设t1s时AB第一次切⊙O于C
连OA、OC
∵PA:PB=4t:5t=4:5=PQ:PO
∴△PAB∽△POQ
又AC、AQ都与⊙O相切
易证ACOQ是正方形
∴PA=8-6=2=4t1
t1=0.5s
设t2s时AB第二次切⊙O于C'
连OC'
同理可证OC'BQ是正方形
PB=4t2=8+6=14
t2=3.5 s
题4： 【如图，已知⊙O的半径为6cm，射线PM经过点O，OP=10cm，射线PN与⊙O相切于点Q．A，B两点同时从点P出发，点A以5cm/s的速度沿射线PM方向运动，点B以4cm/s的速度沿射线PN方向运动．设运动时间为ts．】[数学科目]
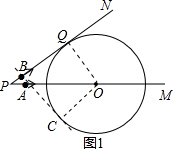（1）连接OQ，
∵PN与⊙O相切于点Q，
∴OQ⊥PN，
即∠OQP=90°，（2分）
∵OP=10，OQ=6，
∴PQ=
10
2?6
2=8（cm）．（3分）（2）过点O作OC⊥AB，垂足为C，
∵点A的运动速度为5cm/s，点B的运动速度为4cm/s，运动时间为ts，
∴PA=5t，PB=4t，
∵PO=10，PQ=8，
∴PAPO＝PBPQ，
∵∠P=∠P，
∴△PAB∽△POQ，
∴∠PBA=∠PQO=90°，（4分）
∵∠BQO=∠CBQ=∠OCB=90°，
∴四边形OCBQ为矩形．
∴BQ=OC．
∵⊙O的半径为6，
∴BQ=OC=6时，直线AB与⊙O相切．
①当AB运动到如图1所示的位置，
BQ=PQ-PB=8-4t，
∵BQ=6，
∴8-4t=6，
∴t=0.5（s）．（6分）
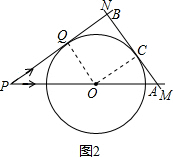
②当AB运动到如图2所示的位置，
BQ=PB-PQ=4t-8，
∵BQ=6，
∴4t-8=6，
∴t=3.5（s）．
∴当t为0.5s或3.5s时直线AB与⊙O相切．（8分）
题5： 如图,已知圆O的半径为8,点A为半径OB延长线上一点,射线AC切圆O于点C,弧BC的长为8/3派求线段AB的长?[数学科目]
r=8
圆周长=16π
所以BC弧所对的圆心角COA=[(8/3)π/16π]*360=60度
AC是切线,所以OA垂直AC
则直角三角形ACO中,角O=60度
所以角A=30度
所以角A所对的直角边OCsh斜边AO的一半
OC=r=8
所以AO=16
BO=r=8
所以AB=16-8=8