【求证有两个角及其中】【求证:有两个角及其中一角的角平分线对应相等的两个..._楚74
编辑: admin 2017-14-06
-
4
在△ABC与△DEF中,∠A=∠D,∠ABC=∠DEF,∠ABC和∠DEF的角平分线分别为BP、EM,BP=EM.
求证:△ABC≌△DEF
证明:BP、EM分别平分∠ABC和∠DEF,又∠ABC=∠DEF
从而∠ABP=∠DEM
又∠A=∠D,BP=EM
因此△ABP≌△DEM9角,角,边0,
得AB=DE
又∠ABC=∠DEF,∠A=∠D
因此△ABC≌△DEF(角,边,角)
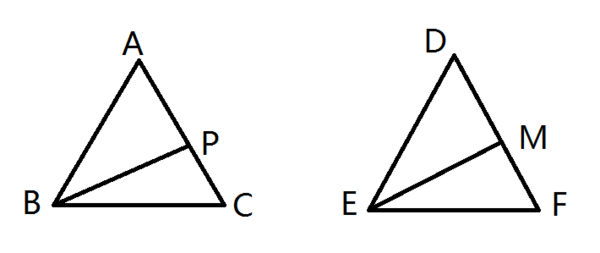
其他同学给出的参考思路:
在△ABC与△DEF中,∠A=∠D,∠ABC=∠DEF,∠ABC和∠DEF的角平分线分别为BP、EM,BP=EM。
求证:△ABC≌△DEF
证明:BP、EM分别平分∠ABC和∠DEF,又∠ABC=∠DEF
从而∠ABP=∠DEM
又∠A=∠D,BP=EM
...
展开
互助这道作业题的同学还参与了下面的作业题
题1: 【求证:有两个角及其中一角的角平分线对应相等的两个三角形全等.要有图的】[数学科目]
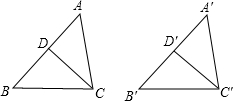
已知:如图△ABC和△A'B'C'中,∠BAC=∠B'A'C',∠B=∠B',AD、A'D'是角平分线,且AD=A'D',
求证:△ABC≌△A'B'C'
证明:∵∠BAC=∠B'A'C,AD、A'D'是角平分线,
∴∠BAD=∠B'A'D’
又∵∠B=∠B',AD=A'D',
∴△ABD≌△A'B'D' (AAS)
∴AB=A'B'
又∵∠B=∠B',∠BAC=∠B'A'C',
∴△ABC≌△A'B'C' (ASA)
题2: 证明:两角分别相等且其中一组等角的对边相等的两个三角形全等.[数学科目]
已知:在△ABC和△DEF中,∠B=∠E,∠C=∠F,AB=DE,
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°
而∠B=∠E,∠C=∠F,
∴∠A=∠D,
在△ABC和△DEF中,
∠A=∠DAB=DE∠B=∠E
∴:△ABC≌△DEF(ASA).
题3: 求证:有两个角及其中一个角的角平分线对应相等的两个三角形全等.[数学科目]
假设:在三角形ABC和三角形ADC中角B等于角D,角A为公共角,AC为公共角平分线,求证:三角形ABC与三角形ADC全等.证明:因为 AC是角A 的角平分线所以,角DAC=角BAC395在三角形ABC和三角形ADC中{角B=角Dl角DAC=角BAC,AC=AC}所以三角形ABC全等于三角形ADCtx
题4: 求证:有两个角何其中一个角的角平分线对应相等的两个三角形全等[数学科目]
利用AAS分别证明出两对小三角形全等 然后同理可以得出两个大三角形全等
题5: 求证:两个角及第三个角的角平分线对应相等的两个三角形全等.[数学科目]
 已知:∠ABC=∠A′B′C′,∠A=∠A′,
已知:∠ABC=∠A′B′C′,∠A=∠A′,
CD、C′D′分别是∠C和∠C′的平分线,且CD=C′D′,
求证:△ABC≌△A′B′C′.
证明:∵∠ABC=∠A′B′C′,∠A=∠A′,
∴∠ACB=∠A′C′B′(三角形内角和定理)
∵CD、C′D′分别是∠C和∠C′的平分线,
∴∠DCB=∠D′C′B′,
∵且CD=C′D′,
在△DCB和△D′C′B′中,∠ABC=∠A′B′C′∠DCB=∠D′C′B′CD=C′D′
∴△DCB≌△D′C′B′(AAS),
∴BC=B′C′,
在△ABC和△A′B′C′中,BC=B′C′∠A=∠A′∠ABC=∠A′B′C′,
∴△ABC≌△A′B′C′.
