【过一点平分三角形面积】怎样过三角形的一边的一点平分三角形面积的做法及证明_数学_vrdgapqk
编辑: admin 2017-14-06
-
4
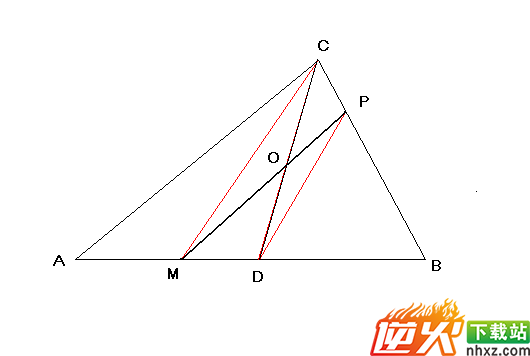
如图,M是△ABC 一条边AB上一点,CD是AB的中线.
连接CM,作DP//CM,那么MP平分△ABC的面积.
因为 CD是一条中线,所以CD平分三角形面积
因为 四边形CMDP是梯形,对角线CD,MP交于O
所以 S△DOM=S△COP
所以 MP平分△ABC的面积
互助这道作业题的同学还参与了下面的作业题
题1: 【证明:过三角形重心的任意一条直线可以把三角形的面积平分.】[数学科目]
这个命题是假的.
比如过重心作一条边的平行线,此时截得面积比为4:5.(可根据相似三角形的性质)
题2: 【请你把下面的三角形分成面积相等的16个小三角形,并说明你的方法是一个三个角为90度,60度和30度的三角形.《小学数学升学夺冠训练A体系》平面图形上的题.最好把图发来】[数学科目]
算了,我还是全部分完吧.
如果不要求三角形全等,那么其实将一边16等份,从等份点向对应的角的顶点连线.这些连线就把三角形分成16个面积相等的小三角形.因为这些小三角形的底和高相等.
如果要求这些小三角形都全等.那么所有的直角三角形都可以.
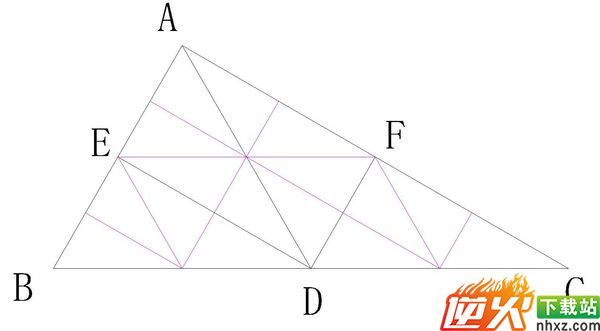
先把大三角形分成4个全等的中等三角形.
∠A是直角.AD是BC上的中线,将△ABC分为大小相等(因为底相等,高公共)的两个等腰三角形ADB和ADC,AD=BD=DC(直角三角形斜边上的中线等于斜边的一半.)
然后从D向AB和AC分别作垂线DE和DF,因为等腰三角形底边上的高也是中线.所以将三角形ADB和ADC分别分成两个全等的三角形.这四个三角形BDE,DEA,DAF,DFC都全等,面积也就相等.而且都是直角三角形.
然后根据刚才的做法,BDE,DEA,DAF,DFC这四个直角三角形又都可以各自分割成4个小的、全等的直角三角形.这样总共就分了4×4=16个全等的直角三角形.
题3: 三角形各种面积公式证明急用!要全的公式和证明![数学科目]
由正弦定理得
sinB=b*(sinA/a)
sinC=c*(sinA/a)
代入得
(1/2)*a^2*[(sinBsinC)/sinA]
=(1/2)*a^2*[(sinA*bc)/a^2]
=(1/2)*bc*sinA=S
所以
S=(1/2)*a^2*[(sinBsinC)/sinA]
题4: 一般三角形面积平分线如何找三角形面积如何被平分?是否交于一点[数学科目]
找出这个三角形一边上的中线,就可以把这个三角形的面积平分.
具体做法:将一个顶点及它的对边的中点连接,这条线段所在的直线就会平分这个三角形面积.
题5: 证明三角形的面积公式
三角形的面积公式有两个:
1/2底乘高
1/2absinC
一般证明要用极限法(高3学的)
